Leonardo Pisano detto il Fibonacci (1175-1250), cioè figlio di Bonaccio, individuò questa serie per la prima volta nel 1202, per risolvere un problema pratico: quante coppie di conigli si ottengono in un anno da una sola coppia supponendo che produca ogni mese (tranne il primo) una nuova coppia che a sua volta diventa fertile a partire dal secondo mese?
La risposta è 144 coppie di conigli. In questa serie ogni numero è il risultato della somma dei due precedenti: 0, 1, 1, 2, 3, 5, 8, 13… fino all’infinito.
Fino al XIX secolo a questa successione non fu attribuita alcuna importanza, finché si scoprì che può essere applicata, per esempio, nel calcolo delle probabilità, nella sezione aurea e nel triangolo aureo. I numeri di Fibonacci si trovano anche in natura, per esempio nella disposizione delle foglie (vedere disegno sopra). In molti alberi, scegliendo una foglia su uno stelo e assegnandole il numero “0”, contando il numero di foglie fino ad arrivare a una perfettamente allineata con la foglia “0”, probabilmente si troverà un numero di Fibonacci.
Le sue proprietà geometriche e matematiche e la frequente riproposizione in svariati contesti naturali e culturali, apparentemente non collegati tra loro, hanno suscitato per secoli nella mente dell’uomo la conferma dell’esistenza di un rapporto tra macrocosmo e microcosmo, tra Dio e l’uomo, l’universo e la natura: un rapporto tra il tutto e la parte, tra la parte più grande e quella più piccola che si ripete all’infinito attraverso infinite suddivisioni.
Diversi filosofi e artisti sono arrivati a cogliervi col tempo un ideale di bellezza e armonia spingendosi a ricercarlo e, in alcuni casi, a ricrearlo nell’ambiente antropico quale canone di bellezza; testimonianza ne è la storia del nome che in epoche più recenti ha assunto gli appellativi di aureo e divino.
|
Oramai è rinomato che la successione di Fibonacci è onnipresente in natura.
“La matematica è l’alfabeto in cui Dio ha scritto l’Universo. La filosofia naturale è scritta in questo grandissimo libro che continuamente ci sta aperto innanzi agli occhi, io dico l’universo, ma non si può intendere se prima non s’impara a intender la lingua e conoscer i caratteri nei quali è scritto. Egli è scritto in lingua matematica, e i caratteri son triangoli, cerchi ed altre figure geometriche, senza i quali mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un oscuro labirinto.” (Galileo Galilei) Quasi tutti i fiori hanno tre o cinque o otto o tredici o ventuno o trentaquattro o cinquantacinque o ottantanove petali: i gigli ne hanno tre, i ranuncoli cinque, la calendula tredici, l’astro ventuno, e le margherite di solito ne hanno trentaquattro o cinquantacinque o ottantanove.
Troviamo i numeri di Fibonacci anche nei fiori di girasole. Le piccole infiorescenze al centro di girasole, che poi si trasformano in semi, sono disposte lungo due insiemi di spirali che girano rispettivamente in senso orario e antiorario. Spesso le spirali orientate in senso orario sono trentaquattro e quelle orientate in senso antiorario cinquantacinque; ma a volta sono rispettivamente cinquantacinque e ottantanove, o addirittura ottantanove e centoquarantaquattro, e si tratta sempre di numeri di Fibonacci consecutivi (il cui rapporto si approssima alla sezione aurea).
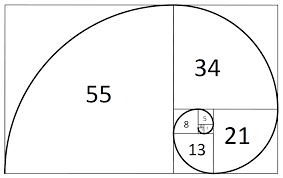
Se si disegna un rettangolo con i lati che stanno in rapporto aureo fra di loro, lo si può dividere in un quadrato e un altro rettangolo, simile a quello grande nel senso che anche i suoi lati stanno fra loro nel rapporto aureo. A questo punto il rettangolo minore può essere diviso in un quadrato e un rettangolo che ha pure i lati in rapporto aureo, e così via. La curva che passa per vertici consecutivi di questa successione di rettangoli è una spirale che troviamo spesso nelle conchiglie e nella disposizione dei semi del girasole sopra descritta e delle foglie su un ramo.
|
|
Questo rettangolo ha proporzioni esteticamente molto gradevoli. La sezione aurea non è presente solo nella natura ma anche nell’arte, come ideale classico della bellezza. C’è qualcosa di divino in essa, tant’è vero che l’odierna Fibonacci Society è diretta da un sacerdote e ha sede presso il St. Mary’s College in California. La società si dedica alla ricerca di esempi di sezione aurea e di numeri di Fibonacci nella natura, in arte e in architettura, basandosi sulla convinzione che il rapporto aureo sia un dono di Dio al mondo. La sezione aurea è presente come ideale di bellezza nel Partenone di Atene; il rapporto fra larghezza e lunghezza nel Partenone corrisponde alla sezione aurea.
.jpg)
Nella Grande Piramide di Giza, costruita molti secoli prima del Partenone, il rapporto fra l’altezza di una faccia e metà di un lato della base corrisponde ancora una volta alla sezione aurea.
Il papiro egizio Rhynd parla di “proporzione sacra”, e diverse statue antiche, al pari di molti dipinti rinascimentali, presentano proporzioni uguali alla sezione aurea, o divina proporzione.
La sezione aurea viene ritenuta un ideale di bellezza che vale anche al di là dei fiori e dell’architettura. In una lettera scritta alla società qualche anno fa, un membro della Fibonacci Society spiegava che una persona nota per cercare la sezione aurea un po’ ovunque aveva chiesto a diverse coppie di fare un esperimento: il marito avrebbe dovuto misurare l’altezza dell’ombelico della moglie, dividendo poi la misura ottenuta per la statura. Secondo lo scrivente, il risultato si avvicinava a 0,618 per tutte le coppie.
Articolo a cura di Il Percorso Profondissimo Fonti:https://it.wikipedia.org/wiki/Sezione_aurea |
